方程的根是使方程左、右兩邊相等的未知數(shù)的取值。一元一次方程的根和解相同,只有一個;一元二次方程根和解不同,根可以是重根,解一定不同,一元二次方程若有2個不同根,又稱有2個不同解;對于多元方程,方程的解不能說成是方程的根,因為多元方程是不存在根的概念。

根的意思就是方程的解。方程的根是使方程左、右兩邊相等的未知數(shù)的取值。一元二次方程根和解不同,根可以是重根,而解一定是不同的,一元二次方程如果有2個不同根,又稱有2個不同解。
方程的根就是方程的解。方程的根是使方程左、右兩邊相等的未知數(shù)的取值。一元二次方程根和解不同,根可以是重根,解一定不同,一元二次方程若有2個不同根,又稱有2個不同解。
另外在解分式方程、無理方程、對數(shù)方程時,需化為整式方程,有時會產(chǎn)生增根——使原方程無意義的未知數(shù)取值,此時該值便不是原方程的解。對于多元方程,方程的根可以叫方程的解,但方程的解不一定可以叫方程的根。
1、定義不同
解,是數(shù)學上的“解”,使得方程中等號兩邊相等的未知數(shù)的值叫做方程的解。
所謂方程的根是使方程左、右兩邊相等的未知數(shù)的取值。
2、一元二次方程中不同
一元二次方程根和解不同,根可以是重根,而解一定是不同的,一元二次方程如果有2個不同根,又稱有2個不同解。
3、類型不同
解:不是所有的方程都有解,或者只有唯一解。有一些方程在實數(shù)的范圍內(nèi)沒有解,稱為無解方程;有一些方程有唯一的解;有一些方程有兩個或者更多特定數(shù)量的解;也有一些方程有無窮個解。
根:重根,在一元方程中方程的解可能會受到某些實際條件的限制,如:一道關于每天生產(chǎn)多少零件的應用題的函數(shù)符合x^2-10x-24=0,此方程的根:x=12,x2=-2,雖然x=-2符合方程的根的條件。
方程是法國數(shù)學家韋達首創(chuàng)。韋達最重要的貢獻是對代數(shù)學的推進,他最早系統(tǒng)地引入代數(shù)符號,推進了方程論的發(fā)展。韋達用“分析”這個詞來概括當時代數(shù)的內(nèi)容和方法。
他創(chuàng)設了大量的代數(shù)符號,用字母代替未知數(shù),系統(tǒng)闡述并改良了三、四次方程的解法,指出了根與系數(shù)之間的關系。給出三次方程不可約情形的三角解法。著有《分析方法入門》、《論方程的識別與訂正》等多部著作。

84消毒液是次氯酸鈉(NaClO),潔廁靈的主要成分是鹽酸(HCl),兩者反應化學方程式為:NaClO+2HCl=NaCl+Cl2↑+H2O...

p+(1/2)*ρv^2+ρgz=C,這個式子被稱為伯努利方程。它也可以被表述為p1+1/2ρv1^2+ρgh1=p2+1/2ρv2^2+ρ...

方程是指含有未知數(shù)的等式。是表示兩個數(shù)學式之間相等關系的一種等式,使等式成立的未知數(shù)的值稱為“解”或“根”。求方程的解的過程稱為“解方程”。...

對的。方程是指含有未知數(shù)的等式,是表示兩個數(shù)學式之間相等關系的一種等式,使等式成立的未知數(shù)的值稱為“解”或“根”。求方程的解的過程稱為“解方...

使方程兩邊相等的未知數(shù)的值叫做方程的解,只含一個未知數(shù)的方程的解,也叫方程的根。方程的根可以叫方程的解,但方程的解不一定可以叫方程的根。方程...
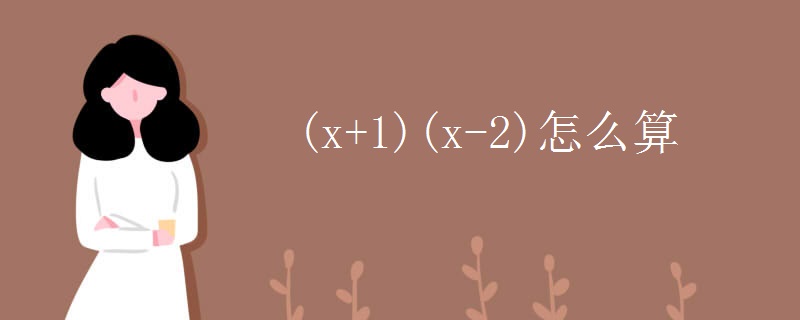
解:(x+1)(x-2)=x2-2x+x-2=x2-x-2。故答案為x2-x-2。方程是指含有未知數(shù)的等式。是表示兩個數(shù)學式(如兩個數(shù)、函數(shù)...

方程是指含有未知數(shù)的等式。是表示兩個數(shù)學式,如兩個數(shù)、函數(shù)、量、運算之間相等關系的一種等式,使等式成立的未知數(shù)的值稱為“解”或“根”;含有等...

方程是指含有未知數(shù)的等式。是表示兩個數(shù)學式(如兩個數(shù)、函數(shù)、量、運算)之間相等關系的一種等式,使等式成立的未知數(shù)的值稱為“解”或“根”。在數(shù)...